Distancias y Punto medio de Rectas

Distancia entre dos puntos

Cuando los puntos se encuentran ubicados sobre el eje x o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas.
Ejemplo: La distancia entre los puntos (-4,0) y (5,0) es 4 + 5 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje y o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:

Para demostrar esta relación se deben ubicar los puntos A(x₁,y₁) y B(x₂,y₂) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa AB y emplear el teorema de pitágoras.

Ejemplo: Calcula la distancia entre los puntos A(7,5) y B (4,1)

d = 5 unidades

Distancia entre un punto y una recta.

 

Dada una recta r:Ax+By+C=0 y P=(p₁,p₂) un punto no contenido en ella. La distancia entre el punto y la recta viene dada por: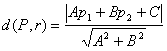
Consideremos la recta r:6x+8y-10=0 y el punto P=(2,1) calculamos la distancia entre ambos.

Punto medio entre dos puntos 

Punto medio entre dos puntos de calculadora es una herramienta en l�nea para el c�lculo de geometr�a anal�tica programado para encontrar el punto medio exacto entre los dos puntos dados por un promedio de las coordenadas XY. El punto medio se define como el punto que se encuentra exactamente a mitad de camino entre dos puntos dados. Los dos coordiantes determinados (x₁, y₁) y (x₂, y₂) en el plano XY se utilizan en esta calculadora para encontrar el punto medio. Entonces la f�rmula para encontrar el punto medio entre dos puntos como sigue

F�rmula del punto medio: M =