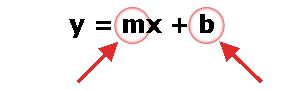EJEMPLO 1: (Términos positivos)
x2 + 6x + 9 = (x + 3)2
x
3
2.3.x
6x
Busco dos términos que sean "cuadrado" de algo. Son:
x2 y 9. Entonces "bajo" la x y
el 3 (las RAICES). Luego verifico 2.x.3 = 6x ("doble producto del primero
por
el segundo"). Dió igual que el otro término. El polinomio es un cuadrado
"perfecto". El resultado de la factorización es la suma de las raices elevada al cuadrado: (x + 3)2
EJEMPLO 2:
x2 + 2x + 1 = (x + 1)2
x
1
2.1.x
2x
Recordemos que el "1" es
cuadrado (de "1" y "-1"). Las raices son: x y 1.
La verificación de que es "perfecto" es 2.x.1 = 2x.
El resultado es (x + 1)2
EJEMPLO 3: (Con fracciones)
x2 + 8/3 x + 16/9 = (x + 4/3)2
x
4/3
2. 4/3 . x
8/3
x
La fracción 16/9 es cuadrado de 4/3. Las raices son x y 4/3.
jueves, 28 de junio de 2012
miércoles, 27 de junio de 2012
Ecuaciones Trigonométricas
Una
ecuación trigonométrica es aquella ecuación en la que aparecen una o más
funciones trigonométricas. En las ecuaciones trigonométricas la incógnita es
el ángulo común de las funciones trigonométricas. No puede especificarse un
método general que permita resolver cualquier ecuación trigonométrica; sin
embargo, un procedimiento efectivo para solucionar un gran número de éstas
consiste en transformar, usando principalmente las identidades
trigonométricas, todas las funciones que aparecen allí en una sola función
(es recomendable pasarlas todas a senos o cosenos). Una vez expresada la
ecuación en términos de una sola función trigonométrica, se aplican los
pasos usuales en la solución de ecuaciones algebraicas para despejar la
función; por último, se resuelve la parte trigonométrica, es decir,
conociendo el valor de la función trigonométrica de un ángulo hay que pasar
a determinar cuál es ese ángulo.


viernes, 22 de junio de 2012
Suma o Diferencia de Cubos Perfectos
| a3 | + | b3 | = | (a + b)(a2 - ab + b2) |
| a | b |
| a3 | - | b3 | = | (a - b)(a2 + ab + b2) | |
| a | b | ||||
Procedimiento para factorizar
|
|||||||||||||||||
| Factorizar
8x3 + 27
La raíz cúbica de : 8x3 es 2x La raíz cúbica de : 27 es 3
Factorizar 64x3 - 1000 La raíz cúbica de : 64x3 es 4x La raíz cúbica de : 1000 es 10
|
|||||||||||||||||
jueves, 21 de junio de 2012
Diferencia de cuadrados
Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.
Al estudiar los productos notables teníamos que:
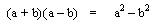 En donde el resultado es una diferencia de cuadrados, para este capitulo es el caso contrario:
En donde el resultado es una diferencia de cuadrados, para este capitulo es el caso contrario:
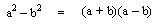 Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.
Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.
Pasos:
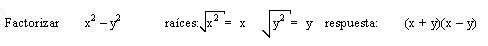 Ejemplos:
Ejemplos:
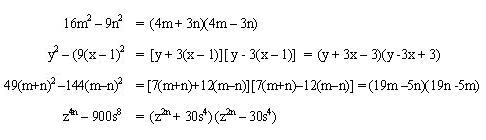
Al estudiar los productos notables teníamos que:
Pasos:
- Se extrae la raíz cuadrada de ambos términos.
- Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo).
Ecuaciones exponenciales
Las
funciones exponencial y logarítmica son las que tienen más
presencia en los fenómenos observables, por lo que existen
diversidad de situaciones cuyo estudio implica el planteamiento
de ecuaciones exponenciales o logarítmicas.
Ejemplo de ello es la escala Rither. En ella se define la magnitud M de un terremoto en función de la amplitud A de sus ondas superficiales así: M=log A+C donde C =3,3+1,66 logD-logT es una constante que depende del periodo T de las ondas registradas en el sismógrafo y de la distancia D de éste al epicentro, en grados angulares. Si quisiésemos saber la amplitud (intensidad) de la onda sísmica tendríamos que resolver una ecuación logarítmica.
También tendríamos que resolver ecuaciones si queremos hallar el número horas necesarias (t) para que la bacteria Escherichia coli presente en el intestino de muchos mamíferos alcance un número concreto. (P=P0.2t/D siendo P= 8000 bacterias, P0 =500 D=30).
Análogamente si queremos hallar la antigüedad de un hueso hallado en un yacimiento arqueológico sabiendo que contiene el 20% del carbono 14 que contenía en vida del animal, tenemos que resolver la ecuación: 0,2=e-0,000121t .
Teorema (Leyes de los Exponentes)




Ejemplo de ello es la escala Rither. En ella se define la magnitud M de un terremoto en función de la amplitud A de sus ondas superficiales así: M=log A+C donde C =3,3+1,66 logD-logT es una constante que depende del periodo T de las ondas registradas en el sismógrafo y de la distancia D de éste al epicentro, en grados angulares. Si quisiésemos saber la amplitud (intensidad) de la onda sísmica tendríamos que resolver una ecuación logarítmica.
También tendríamos que resolver ecuaciones si queremos hallar el número horas necesarias (t) para que la bacteria Escherichia coli presente en el intestino de muchos mamíferos alcance un número concreto. (P=P0.2t/D siendo P= 8000 bacterias, P0 =500 D=30).
Análogamente si queremos hallar la antigüedad de un hueso hallado en un yacimiento arqueológico sabiendo que contiene el 20% del carbono 14 que contenía en vida del animal, tenemos que resolver la ecuación: 0,2=e-0,000121t .
Teorema (Leyes de los Exponentes)
Sean a y b reales positivos ,entonces:
1. 

2. 
3. 
4. 
5.  .
.
6 .
Resolver las ecuaciones exponenciales:
miércoles, 20 de junio de 2012
martes, 19 de junio de 2012
Demostración de Identidades Trigonométricas
Dada una proposición trigonométrica, demostrarla consiste en transformarla hasta convertirla
en una igualdad que sea cierta sin lugar a dudas.
Para que una igualdad trigonométrica quede demostrada se debe llegar a:
1) una identidad, es decir, a algo igual a sí mismo; o bien
2) a una cualquiera de las fórmulas trigonométricas.
Recuerda que para demostrar identidades, no sólo debo contar con los conocimientos básicos de trigonometría, sino también con el conocimiento de operaciones con expresiones algebraicas, factorización productos notables, operaciones con fracciones, entre otros.
Debes agregarle otros ingredientes muy valiosos: mucha astucia, un poco de ingenio y bastante razonamiento lógico.
en una igualdad que sea cierta sin lugar a dudas.
Para que una igualdad trigonométrica quede demostrada se debe llegar a:
1) una identidad, es decir, a algo igual a sí mismo; o bien
2) a una cualquiera de las fórmulas trigonométricas.
Recuerda que para demostrar identidades, no sólo debo contar con los conocimientos básicos de trigonometría, sino también con el conocimiento de operaciones con expresiones algebraicas, factorización productos notables, operaciones con fracciones, entre otros.
Debes agregarle otros ingredientes muy valiosos: mucha astucia, un poco de ingenio y bastante razonamiento lógico.
Ecuación de la recta punto-pendiente
Esta forma de obtener la ecuación de una recta se suele utilizar
cuando se conocen su pendiente y las coordenadas de uno solo de sus
puntos.
Entonces, la ecuación de la recta que pasa por el punto P1 = (x1, y1) y tiene la pendiente dada m, se establece de la siguiente manera:
Hallar la ecuación de la recta que pasa por el punto A (2, – 4) y que tiene una pendiente de – 1/3
Al sustituir los datos en la ecuación, resulta lo siguiente:
y – y1 = m(x – x1)
y – (–4) = – 1/3(x – 2)
3(y + 4) = –1(x – 2)
3y + 12 = –x + 2
3y +12 + x – 2 = 0
3y + x + 10 = 0
x + 3y + 10 = 0 Forma General
y = -1/3 x- 10/3 Forma Particular
Entonces, la ecuación de la recta que pasa por el punto P1 = (x1, y1) y tiene la pendiente dada m, se establece de la siguiente manera:
y – y1 = m(x – x1)
EjemploHallar la ecuación de la recta que pasa por el punto A (2, – 4) y que tiene una pendiente de – 1/3
Al sustituir los datos en la ecuación, resulta lo siguiente:
y – y1 = m(x – x1)
y – (–4) = – 1/3(x – 2)
3(y + 4) = –1(x – 2)
3y + 12 = –x + 2
3y +12 + x – 2 = 0
3y + x + 10 = 0
x + 3y + 10 = 0 Forma General
y = -1/3 x- 10/3 Forma Particular
lunes, 18 de junio de 2012
Ecuación de la recta
Ecuación de una recta
La ecuación GENERAL de una línea recta tiene la forma:
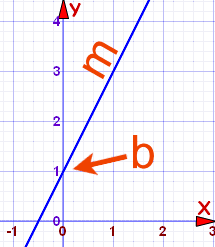
y = mx + b
¿Qué significa?
 |
|
|||||
|
y = cuánto arriba
x = cuán lejos
m = gradiente o pendiente (cuán inclinada es la línea)
b = la intersección Y (donde la línea se cruza con el eje Y)
La ecuación de la recta también la podemos expresar con todos los
términos en lado izquierdo de la ecuación, igualados a cero. Es lo que
se denomina: Ecuación general o implícita de la recta:
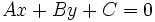
| ||||||
Logaritmos
En matemática, el logaritmo de un número en una base determinada es el exponente al cual hay que elevar la base para obtener el número. Es la función matemática inversa de la función exponencial.
Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo (base b) se ha de elevar para obtener dicho argumento. Es la función inversa de la exponencial x = bn. Esta función se escribe como: n = logb x, lo que permite obtener n. Así, en la expresión 102 = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log10 100 = 2.
Por ejemplo:
Se denomina logaritmo neperiano (ln) o logaritmo natural al logaritmo en base e de un número o resultado dado por el exponente.
Propiedades de los logaritmos
El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
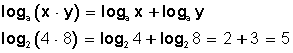
El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:
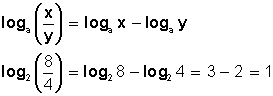
El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:
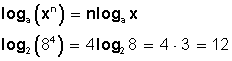
El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:
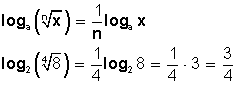
viernes, 15 de junio de 2012
Factorización: Factor Común
FACTOR COMÚN
Se dice que un polinomio tiene factor común cuando una misma
cantidad, ya sea número o letra, se encuentra en todos los términos del
polinomio.
Si en todos los términos de un polinomio figura un factor
común, dicho polinomio es igual al producto de ese factor por el
polinomio que resulta al dividir cada término por ese factor.
Para efectuar el factor común hay que tomar en cuenta que
este se realiza tanto para los números como para las letras, y con las
letras se toma la que tenga el menor exponente de todas.
Ejemplo:
Como puede verse el cinco es el común numérico y la “x” la
única letra común en este polinomio, como dos es el menor exponente de
“x” es este el exponente que se tomara en cuenta, siendo el factor común
5x2.
Nos queda como respuesta:
Nos queda como respuesta:
Ejemplos:
Encontrar el factor común de los siguientes términos:
Encontrar el factor común de los siguientes términos:
miércoles, 13 de junio de 2012
martes, 12 de junio de 2012
Otras identidades trigonométricas
Identidades de ángulo doble
|
Sen 2Ө= 2senӨ . cosӨ
Cos 2Ө= 1 –
2sen2Ө
|
Identidades para la suma
|
Sen(x+y) = senx . cosy + cosx . seny
Cos(x+y)= cosx . cosy – senx . seny
Tan(x+y)= (tanx+tany) / (1 – tanx .
tany)
|
martes, 5 de junio de 2012
Solución de problemas sobre sistemas de ecuaciones
http://www.juntadeandalucia.es/averroes/iesdiegogaitan/departamentos/departamentos/departamento_de_matemat/recursos/algebraconpapas/recurso/tests/sistemasproblemas/sisprob01.htm
miren como se plantea el sistema y contesten las actividades de la página.
miren como se plantea el sistema y contesten las actividades de la página.
Suscribirse a:
Entradas (Atom)